Na čo sa používajú epicyklické ozubené kolesá？

Epicyklické ozubené kolesáTiež známe ako planétové prevodové systémy, sú široko používané v rôznych odvetviach vďaka svojej kompaktnej konštrukcii, vysokej účinnosti a všestrannosti.

Tieto prevody sa používajú predovšetkým v aplikáciách, kde je obmedzený priestor, ale je nevyhnutný vysoký krútiaci moment a variabilita otáčok.

1. Automobilové prevodovky: Epicyklické ozubené kolesá sú kľúčovou súčasťou automatických prevodoviek, ktoré zabezpečujú plynulé radenie prevodových stupňov, vysoký krútiaci moment pri nízkych rýchlostiach a efektívny prenos výkonu.
2. Priemyselné stroje: Používajú sa v ťažkých strojoch pre svoju schopnosť zvládať vysoké zaťaženie, rovnomerne rozkladať krútiaci moment a efektívne pracovať v kompaktných priestoroch.
3. Letectvo: Tieto ozubené kolesá zohrávajú kľúčovú úlohu v leteckých motoroch a rotoroch vrtuľníkov, čím zabezpečujú spoľahlivosť a presné riadenie pohybu v náročných podmienkach.
4. Robotika a automatizácia: V robotike sa epicyklické prevody používajú na dosiahnutie presného riadenia pohybu, kompaktného dizajnu a vysokého krútiaceho momentu v obmedzených priestoroch.

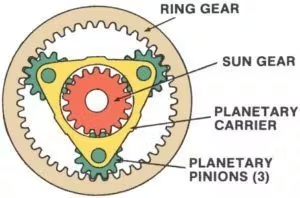
Aké sú štyri prvky epicyklického ozubeného kolesa?

Epicyklické ozubené koleso, tiež známe akoplanétový prevod systém je vysoko účinný a kompaktný mechanizmus bežne používaný v automobilových prevodovkách, robotike a priemyselných strojoch. Tento systém sa skladá zo štyroch kľúčových prvkov:

1. Sun GearCentrálne koleso, umiestnené v strede ozubeného kolesa, je primárnym hnacím motorom alebo prijímačom pohybu. Priamo zaberá s planétovými kolesami a často slúži ako vstup alebo výstup systému.

2. Planétové prevodyIde o viacero ozubených kolies, ktoré sa otáčajú okolo centrálneho kolesa. Sú namontované na unášači planét a zaberajú s centrálnym aj korunovým kolesom. Planétové kolesá rovnomerne rozkladajú zaťaženie, vďaka čomu je systém schopný zvládať vysoký krútiaci moment.

3.Nosič planétTento komponent drží planétové kolesá na mieste a podporuje ich rotáciu okolo centrálneho kolesa. Unášač planét môže pôsobiť ako vstupný, výstupný alebo stacionárny prvok v závislosti od konfigurácie systému.

4.Ozubený veniecIde o veľké vonkajšie ozubené koleso, ktoré obopína planétové kolesá. Vnútorné zuby ozubeného vence zaberajú s planétovými kolesami. Rovnako ako ostatné prvky, aj ozubený veniec môže slúžiť ako vstup, výstup alebo môže zostať nehybný.

Súhra týchto štyroch prvkov poskytuje flexibilitu na dosiahnutie rôznych rýchlostných pomerov a zmien smeru v rámci kompaktnej konštrukcie.

Ako vypočítať prevodový pomer v epicyklickej prevodovke?

Prevodový pomerepicyklické ozubené koleso závisí od toho, ktoré komponenty sú pevné, vstupné a výstupné. Tu je podrobný návod na výpočet prevodového pomeru:

1. Pochopte konfiguráciu systému:

Určte, ktorý prvok (Slnko, nosič planéty alebo prstenec) je stacionárny.

Určte vstupné a výstupné komponenty.

2. Použite základnú rovnicu prevodového pomeru: Prevodový pomer epicyklického ozubeného kolesa možno vypočítať pomocou:

GR = 1 + (R / S)

Kde:

GR = Prevodový pomer

R = Počet zubov na ozubenom venci

S = Počet zubov na centrálnom kolese

Táto rovnica platí, keď je výstupom unášač planét a buď centrálne koleso, alebo ozubený veniec sú nehybné.

3. Úprava pre ďalšie konfigurácie:

• Ak je centrálne koleso nehybné, výstupná rýchlosť systému je ovplyvnená prevodovým pomerom korunového kolesa a unášača planét.
• Ak je ozubený veniec nehybný, výstupná rýchlosť je určená vzťahom medzi centrálnym ozubeným kolesom a unášačom planét.

4. Prevodový pomer medzi výstupom a vstupom: Pri výpočte zníženia rýchlosti (vstup vyšší ako výstup) je pomer jednoduchý. Pri násobení rýchlosti (výstup vyšší ako vstup) invertujte vypočítaný pomer.

Príklad výpočtu:

Predpokladajme, že prevodový stupeň má:

Ozubený veniec (R): 72 zubov

Centrálne ozubené koleso (S): 24 zubov

Ak je unášač planét výstupom a centrálne koleso je nehybné, prevodový pomer je:

GR = 1 + (72/24) GR = 1 + 3 = 4

To znamená, že výstupná rýchlosť bude 4-krát nižšia ako vstupná rýchlosť, čo zabezpečí redukčný pomer 4:1.

Pochopenie týchto princípov umožňuje inžinierom navrhovať efektívne a všestranné systémy prispôsobené špecifickým aplikáciám.